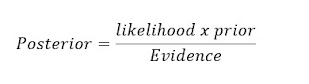Analisis Klasifikasi Algoritma Naive Bayes
ANALISIS KLASIFIKASI ALGORITMA NAÏVE BAYES
Teori keputusan bayes adalah pendekatan statistic yang fundamental dalam pengenalan pola. Pendekatan ini didasarkan pada untifikasi trade-off antaa berbagai keputusan klasifikasi dengan menggunakan probabilitas dan ongkos yang ditimbulkan dalam keputusan tersebut.
Naïve Bayes Adalah suatu klasifikasi berpeluang sederhana berdasarkan aplikasi teorema Bayes dengan asumsi antar variabel penjelas saling bebas (independen). Naïve Bayes juga termasuk dalam kategori supervised learning seperti yang sudah dijelaskan pada Materi 3.
Baca juga : Apa itu Supervised Learning ?
Ciri utama dari algoritma naïve bayes ini adalah asumsi yg sangat kuat (naïf) akan independensi dari masing-masing kondisi / kejadian.
Bayes Learning
Misalkan kita mempunyai masalah yang bersifat hipotesis, yaitu menggambarkan suatu fungsi klasifikasi untuk memisahkan dua jenis obyek ikan bandeng dan Gurami. Kedua objek itu berjaan melalui conveyor. Seorang petani mengamatai objek tersebut lewat di conveyor secara random. Pengamat ini ingin memprediksi ikan apa yang akan lewat selanjutnya. Dalam hal ini h1 mewakili ikan bandeng dan h2 menyatakan ikan gurami. Karena apa yang akan muncul bersifat probabilistic, maka h adalah suatu variabel yang harus dideskripsikan secara probailistik atau peluang. Jika jumlah ikan bandeng dan gurami yang ditangkap sebelumnya sama, maka peluang keduanya yang lewat conveyor tersebut kemungkinan sama besar.
Dalam banyak kasus, kita akan mengambil keputusan dengan informasi yang lebih banyak, tidak sekedar dengan nilai jumlah peluang saja. Dalam contoh ini mungkin kita bisa menggunakan informasi warna, kita beri labe x. sebagai tambahan atribut untuk meningkatkan akurasi prediksi kita.
Dalam hal ini bisa dinamakan fungsi padat peluang sering juga disebut dengan istilah likelihood dari variable h terhadap x. dari tambahan informasi berupa likelihood P(x|h),dan atribut warna, x kita bisa mendapatkan probabilitas posterior sebagai berikut ;
Dimana P(hj|x) menyatakan probabilitas posterior muncul hj jika diketahui x. sedangkan evidence dalam kasus kategori dua kelas tersebut adalah :
dengan bentuk yang lebih umum, formula atau rumus Bayes bisa dijabarkan sebagai berikut :
Contoh Kasus
Sebagai contoh tabel dibawah ini ada contoh dari model dataset training atau data yang digunakan untuk pelatihan seperti yang dijelaskan di materi sebelumnya tentang
Baca juga : Machine Learning, Supervised Dan Unsupervised Learning
Dalam tabel tersebut, ada 13 titik data yang menunjukkan data dengan output Lama Studi Tepat atau Terlambat. Setiap data ditandai dengan atribut sekolah, gender, asal daerah, rerata sks dan bimbel. Kita menggunakan Naïve Bayes untuk menentukan kelas atau keputusan dari data berikut :
Sekolah = SMA, Gender = Pria, Asal Daerah = Jombang, Rerata SKS = SKS<=18, Bimbel = Tidak, Lama Studi = ?
Yang mana kombinasi ini tidak ada dalam tabel tersebut. Dengan menggunakan persamaan Naïve Bayes, kita dapat hitung sebagai berikut.
• Probabilitas prior P(hj)
P(Tepat) = Jumlah Data “Tepat” dibagi Jumlah Data
= 8 : 13 = 0,62= 62%
P(Terlambat) = Jumlah Data “Terlambat” dibagi Jumlah Data
= 5 : 13 = 0,38= 38%
• Probabilitas likelihood
P(sekolah = SMA|Tepat) atau Jumlah data Sekolah “SMA” dengan keterangan “TEPAT” dibagi jumlah data TEPAT
= 2 / 8 =0,25
P(sekolah = SMA|Terlambatt) atau Jumlah data Sekolah “SMA” dengan keterangan “TERLAMBAT” dibagi jumlah data TERLAMBAT
= 2 / 5 = 0,4
Lakukan tahap ini seterusnya pada masing-masing atribut atau likelihood seperti yang digambarkan pada tabel diatas
Jika sudah kita teruskan, maka selanjutnya kita tinggal mencari atau menentukan prediksi dari data yang belum diketahui label kelasnya
Sekolah = SMA, Gender = Pria, Asal Daerah = Jombang, Rerata SKS = SKS<=18, Bimbel = Tidak, Lama Studi = ?
Maka selanjutnya kita kalikan semua variabel dari masing-masing label. Pertama kita kalikan probabilitas dari prior atau label TEPAT
P(TEPAT) = P(tepat) * p(sekolah = SMA|tepat) *p(Gender = Pria|tepat) * p(asal daerah =Jombang|tepat) * p(rerata_sks = sks<=18|tepat) * p(bimbel = Tidak|tepat)
= 0,63 * 0,25 * 0,63 * 0,5 * 0,38 * 0,13 = 0,00225
Kemudian kita kalikan variabel dari nilai probabilias dari prior atau lebel TERLAMABAT
P(TERLAMBAT) = P(terlambat) * p(sekolah = SMA|terlambat) *p(Gender = Pria|terlambat) * p(asal daerah =Jombang|terlambat) * p(rerata_sks = sks<=18|terlambat) * p(bimbel = Tidak|terlambat)
= 0,38 * 0,40 * 0,8 * 0,4 * 0,4 * 1 = 0,03
Jadi nilai P(TERLAMBAT) > P(TEPAT), maka data tersebut akan kita prediksi dengan prior atau kelas atau label atau keputusan “Lama Studi = Terlambat”
Materi Naïve bayes sampai disini dulu, kalau teman-teman belum bisa memahami secara teks tertulis,kalian bisa simak langsung video tutorial diyoutube dibawah ini.
Satu Kata " Jangan Lupa Bernafas dan Tetap Bersyukur "
See You