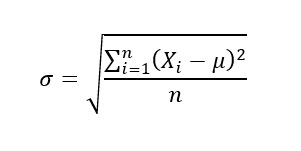Menghitung Naive Bayes Atribut Data Kontinu
ANALISIS ATRIBUT DATA KONTINU AGORITMA NAIVE BAYES
Dari penjelasan sebelumnya tentang analisis algoritma naïve bayes atau bahkan dari kebanyakan materi serta penjelasan naïve bayes saat ini, kita masih menggunakan data dengan atribut nilai diskrit misalnya kalian bisa lihat di
Baca juga : Analisis algoritma Naïve Bayes
Dasar awal dari algoritma Naive Bayes adalah mengklasifikan sebuah nilai peluang atau probabilitas dari sebuah set data. Hal ini bisa dilakukan klasifikasi apabila data tersebut bernilai diskrit atau polynominal. Di praktek lapangan nanti, banyak kemungkinan atribut data yang didapatkan bernilai kontinyu atau numerik, misalnya pada kasus data retensi mahasiswa yang variable nilai SKS, nilai Indeks Prestasi Komulatif atau IPK, Jumlah mata kuliah yang ditempuh dll. Untuk kasus seperti ini kemungkinan setiap nilai adalah unik, dalam artihanya ada satu saja yang nilainya sama.
Dalam beberapa kasus seperti yang telah ditulis Eko Prastetyo dalam buku yang berjudul Data Mining, Mengolah Informasi Menggunakan Matlab. Untuk mencari nilai peluang dari atribut data yang bersifat numerik atau kontinyu. Untuk penyelesaiannya adalah dengan mencari nilai rata-rata dan nilai tengah yang sering muncul dan untuk menghadapi atribut kontinyu tersebut, ada beberapa cara yang dapat dilakukan. diantaranya adalah
- Mendekritkan atribut data kontinyu,misalnya pada atribut cuaca didapatkan data bersifat numerik dengan nilai minimalnya 15°C dan maksimalnya 37,5°C. kita mendeskritkan data tersebut, contoh menjadi 3 kategori,yakni dingin, sedang dan panas. Jadi misalnya nilai antara 15-22°C masuk kategori dingin, 22-29°C masuk kategori sedang dan 29-38°C masuk kategori panas.
• hj = likelihood atau nilai (atribut|hj)
• σ = Standar Deviasi dari atribut (atribut|hj)
• µ = mean atau rata-rata dari (atribut|hj)
Jadi untuk masing-masing (atribut|hj), kita akan menghitung nilai mean(rerata) dan standar deviasi. Nilai ini kita hitung selama proses training, selanjutnya akan kita simpa dan gunakan saat testing yaitu dengan menggunakan fungsi Gaussian.
Untuk kasus nomer satu tadi, misalnya atribut temperature kita ingin mengitung peluang atau probabilitas P(temperature=22,6°C|bermain), maka kita perlu nilai mean (rerata) temperature saat data atau label kelasnya “bermain” dan juga nilai standar deviasinya.
Adapun formula atau rumus dari mean adalah
Dimana jumlah atribut n dengan nilai X dibagi dengan Jumlah n. Selanjutnya adala nilai Standar Deviasi (STD) dan yang kita hitung adalah nilai varian yang mempresentasikan seluruh populasi, maka formula yang bisa kita pakai adalah sebagai berikut
Keterangan:
σ = varian satau ragam untuk populasi
xi = Titik tengah nilai dalam satu atribut
μ = rata-rata atau mean dari populasi
n = Jumlah data
setelah kalian sudah menghitung dari masing-masing atribut dengan dua formula diatas,selanjutnya adalah menghitung dengan formula Gaussian di atas.
Jadi ada dua tahapan jika ingin menggunakan algoritma naive bayes pada kasus atribut data bernilai numerik atau kontinyu, yaitu
- Mendiskritkan data yang bernilai kontinu
- Menggunakan Fungsi Gaussian untuk menentukan nilai probabilitas dalam distribusi normal.
Menurut saya pribadi jika menggunakan model tahapan nomor 1 itu akan memakan banyak waktu, karena harus mencari nilai reratanya dan nilai yang sering muncul, kemudiian mendiskritkan menjadi nilai data polynominal, kemudian di hitung nilai probabilitasnya menggunakan tearoma bayes. Dan apabila menggunakan fungsi gaussian maka, kita hanya tinggal mencari nilai standar deviasi dan mean untuk menentukan nilai probabilitasnya.
Dowload Juga Source Code Naive Bayes atribut data numerik
Kelemahan Naive Bayes Pada Data Kontinyu.
Kelemahan dari penggunaan algoritma naive bayes pada data yang bernilai kontinyu atau numerik adalah jika jumlah nilai kelas tidak seimbang, dalam contoh jika dalam set data kita ada dua kelas antara Positif dan Negatif dan jumlah data tersebur tidak seimbang atau lebih besar dari salah satu kelas saja. Maka naive bayes akan memberikan nilai peluang yang ambigu dan akan menyebabkan kineja dari naive bayes akan memiliki performa yang buruk.
Oke jika kalian sudah bisa memahami teori diatas, kalian juga bisa belajar secara detail tentang Perhitungan Naïve Bayes Atribut Data Kontinyu Dengan Menggunakan MS.Excel pada video dibawah ini.
Nah, Berikut daftar kumpulan teori data mining yang akan kami kemas dari METERI 1 hinggan selesai
MATERI 7. KONSEP DECISION TREE
JIka teman-teman sudah belajar tentang cara menghitung algoritma naive bayes dengan data kontinyu atau numerik. teman-teman juga bisa mengunduh file excel seperti yang ada pada video di atas. link nya ada pada unduh bewarna excel.
Terimakasih sudah percaya dan mau belajar sendiri. untuk menghindari kesalah pahaman diantara beribu bintang hanya kau lah yang paling terang.. awowok :)
Untuk link password file excelnya kalian bisa menghubungi w.a (085784808281)
Rp. 30.000 untuk ganti biaya kopi sama wifi membuat draf file excelnya :). Matur sembah nuwun.
MATERI 1. MENGAPA PERLU DATA MINING ?
MATERI 2. TUGAS – TUGAS DATA MINING
MATERI 3. MACHINE LEARNING, SUPERVISED DAN UNSUPERVISED LEARNING
MATERI 4. CONFUSION MATRIX
MATERI 5. ANALISIS KLASIFIKASI ( ALGORITMA NAIVE BAYES )MATERI 7. KONSEP DECISION TREE
Terimakasih sudah percaya dan mau belajar sendiri. untuk menghindari kesalah pahaman diantara beribu bintang hanya kau lah yang paling terang.. awowok :)
Untuk link password file excelnya kalian bisa menghubungi w.a (085784808281)
Rp. 30.000 untuk ganti biaya kopi sama wifi membuat draf file excelnya :). Matur sembah nuwun.